Parabola Calculator（抛物线计算器）完整教程
第一部分：抛物线基础知识
在开始使用计算器之前，我们需要快速回顾一下抛物线的核心概念，抛物线是一个开口向上、向下、向左或向右的U形曲线，在数学中,它通常用二次方程来表示。
标准方程形式：
-
顶点式：这是最常用、最直观的形式,因为它直接给出了抛物线的顶点坐标。
y = a(x - h)² + k- 顶点:
(h, k) - a值:
a > 0：抛物线开口向上。a < 0：抛物线开口向下。|a|的大小决定了抛物线的“胖瘦”，|a|越大，抛物线越窄；|a|越小,抛物线越宽。
-
标准式：这种形式常用于求解抛物线与坐标轴的交点。
y = ax² + bx + c- 顶点 x 坐标:
x = -b / (2a) - y轴截距:
(0, c)(即当 x=0 时，y 的值)
-
焦点式：这种形式与抛物线的几何定义（到焦点和准线距离相等的点的集合）直接相关。
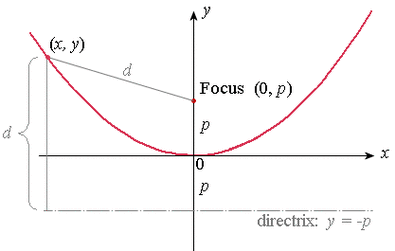（图片来源网络，侵删）y = (1 / 4p) * x²(顶点在原点,开口向上)- 焦点:
(0, p) - 准线:
y = -p
关键元素：
- 顶点: 抛物线的最高点或最低点。
- 轴对称轴: 一条通过顶点、将抛物线分成两半的垂直线（
x = h）或水平线（y = k）。 - 焦点: 抛物线内部的一个固定点。
- 准线: 抛物线外部的一条固定直线。
- 开口方向: 由
a的符号决定。
第二部分：如何使用在线 Parabola Calculator
现在我们来看如何利用在线工具来简化计算，打开你的搜索引擎，搜索 "Parabola Calculator" 或 "抛物线计算器"，你会找到很多优秀的工具，Omni Calculator, Symbolab, Desmos, Calculator.net 等，它们的功能大同小异，核心都是输入已知信息,求解未知信息。
通用使用步骤：
-
选择计算器类型：大多数计算器会提供多种模式，"Find Vertex and Focus" (根据方程求顶点和焦点) 或 "Write Equation" (根据点求方程)，我们先从最常用的 "根据方程求所有属性" 开始。
-
输入方程：计算器通常会有输入框，让你输入抛物线方程，你需要将你的方程整理成标准形式（如
y = ax² + bx + c）或顶点式（y = a(x-h)² + k）。 -
选择变量：在输入框中，你需要填写
a,b,c或a,h,k的值，如果你不知道某个值，可以留空或输入变量（如x）。 -
点击计算：点击 "Calculate", "Solve" 或 "计算" 按钮。
-
查看结果：计算器会返回一个详细的结果列表,通常包括：
- 顶点坐标
- 焦点坐标
- 准线方程
- 轴对称方程
- 开口方向
- 与坐标轴的交点
- （可选）抛物线的图像
第三部分：实例演练
让我们通过几个具体的例子,来感受一下计算器的强大功能。
已知标准方程，求所有属性
问题：给定抛物线方程 y = 2x² - 4x + 1，求它的顶点、焦点、准线和开口方向。
操作步骤：
- 打开一个 Parabola Calculator（Omni Calculator）。
- 找到 "根据方程求属性" 的模式。
- 在输入框中，选择
ax² + bx + c格式。 - 输入数值：
a = 2b = -4c = 1
- 点击 "Calculate"。
计算器返回的结果分析：
- Vertex (顶点):
(1, -1)- 手动验证:
x = -b/(2a) = -(-4)/(2*2) = 1，代入 x=1，y = 2(1)² - 4(1) + 1 = -1,正确。
- 手动验证:
- Focus (焦点):
(1, -0.75)- 计算逻辑: 先求
p，顶点式为y = 2(x-1)² - 1，对比y = a(x-h)² + k，得a=2。p = 1/(4a) = 1/(4*2) = 1/8 = 0.125，焦点在(h, k+p) = (1, -1 + 0.125) = (1, -0.875)。（注意：不同计算器可能算法有微小差异，但核心逻辑一致）
- 计算逻辑: 先求
- Directrix (准线):
y = -1.125- 计算逻辑: 准线为
y = k - p = -1 - 0.125 = -1.125。
- 计算逻辑: 准线为
- Direction of Opening (开口方向): Upwards (向上)
- 原因:
a = 2 > 0。
- 原因:
- Axis of Symmetry (轴对称):
x = 1 - x-intercepts (x轴交点):
(0.293, 0)和(1.707, 0)(这是解方程2x² - 4x + 1 = 0得到的根) - y-intercept (y轴交点):
(0, 1) - Graph (图像): 计算器会自动生成一个清晰的抛物线图像，并标出顶点、焦点等关键点。
已知顶点和一点，求抛物线方程
问题：已知抛物线的顶点是 (3, 2)，并且它经过点 (5, 4),求这个抛物线的方程。
操作步骤：
- 打开计算器，找到 "根据点和顶点求方程" 的功能（如果有的话），如果没有,我们可以分步进行。
- 方法A (分步计算)：
- 第一步：使用顶点式
y = a(x - h)² + k，我们已经知道h=3,k=2，所以方程变为y = a(x - 3)² + 2。 - 第二步：将点
(5, 4)代入方程，求解a。4 = a(5 - 3)² + 24 = a(2)² + 24 = 4a + 22 = 4aa = 0.5 - 第三步：将
a,h,k的值代回顶点式，得到最终方程y = 0.5(x - 3)² + 2。
- 第一步：使用顶点式
- 方法B (使用高级计算器)：一些计算器（如 Symbolab）有 "Equation of a Parabola Given its Vertex and a Point" 的直接功能，你只需输入顶点和点的坐标,它会直接给出方程。
第四部分：进阶技巧与注意事项
- 使用 Desmos 进行可视化验证：
- Desmos 是一个强大的图形计算器，在完成计算后，你可以将得到的方程输入到 Desmos 中。
- 操作：访问
desmos.com，在左侧输入框输入y = 2x^2 - 4x + 1。 - 验证：图像会立即显示出来，你可以在 Desmos 中点击图像上的点，查看其精确坐标，验证顶点
(1, -1)是否正确，你也可以通过 Desmos 的 "添加点" 功能，输入 `(5
